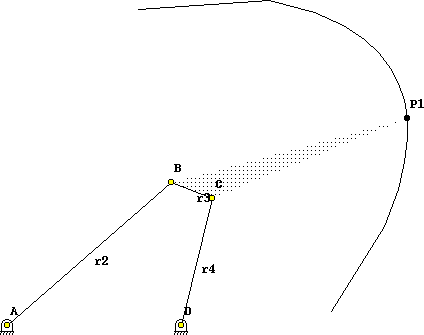

This type of Grashof linkage is obtained when the shortest link is the floating link (r3). Both the input and output links have limited ranges of motion that are defined as follows:
Input Link
lower limit: theta2 = theta1 + theta2'
upper limit: theta2 = theta1 + theta2''
where theta2' = acos [ ( r1^2 + r2^2 - ( r3 - r4 )^2 ) / ( 2 * r1 * r2 ) ]
and
theta2'' = acos [ ( r1^2 + r2^2 - ( r3 + r4 )^2 ) / ( 2 * r1 * r2 ) ]
Output Link
lower limit: theta4 = 180 + theta1 - theta4''
upper limit: theta4 = 180 +theta1 - theta4'
where theta4' = acos [ ( r1^2 + r4^2 - ( r3 - r2 ) ^2 ) / ( 2 * r1 * r4 ) ]
and
theta4'' = acos [ ( r1^2 + r4^2 - (r3 + r2)^2 ) / (2*r1*r4) ]
To see animations of this linkage select the links below: