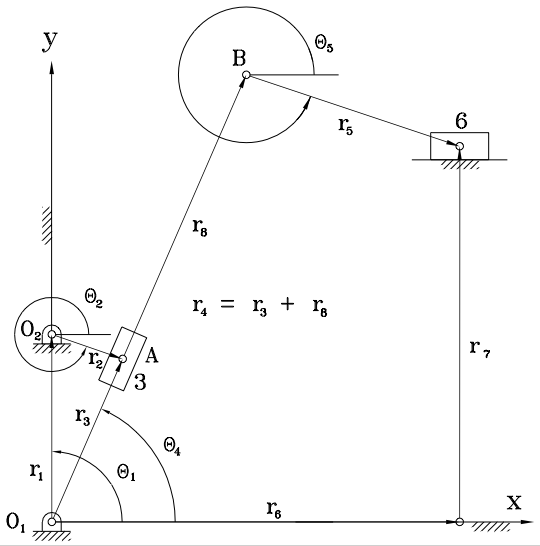
With the specifications for the mechanism given here,
plot the velocity of the output slider versus time and display
an animation of the mechanism in action.
the links have the following lengths:
r1 = 25 mm, r2 = 10 mm, r4 = 65 mm, r5 = 30 mm, r7 = 50 mm
The ground link, r1, will be at 90°. The angular velocity of the input link is -15 rads per sec.

To solve the problem we'll use the CQuickReturn class that was developed to analyze
this type of mechanism. It has member functions to enter the mechanism specifications
and others that present the output to the user.
The code shown below uses this class.
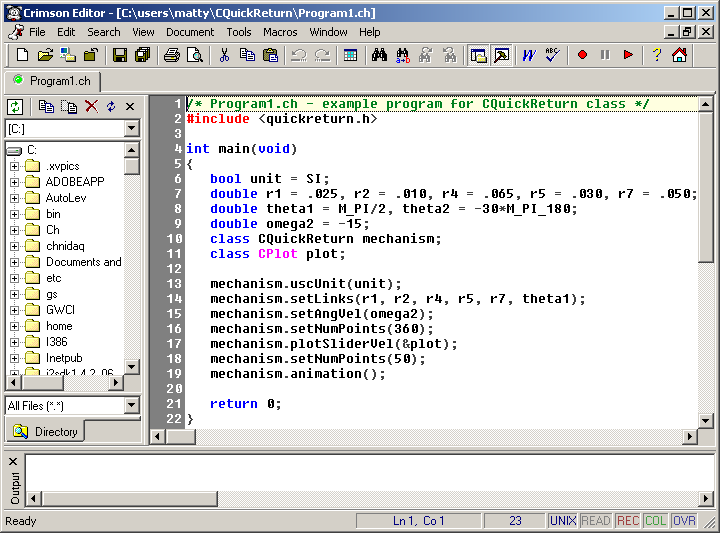
This code can be run using the Crimson Editor as an Integrated Development Environment (IDE) shown above. It allows the execution of Ch programs from this GUI and is free to download. Below we describe how the code interacts with the member functions in the class. The first line of the program
includes the header file quickreturn.h which defines the CQuickReturn class, macros,
and prototypes of member functions. Like all C/C++ programs, the program is started
with the main() function. The next four lines
define the unit type, link lengths, ground and input link angles (in rad), and input link angular velocity (in rad/s) of the quick return mechanism. The lines
construct an object of the CQuickReturn class for the calculations and the CPlot class
to display the output. The following three lines
set the units, dimensions of each link, phase angle for link 1, and velocity of the input link as defined above. One line
is needed to set the number of points to be used for plotting. The line
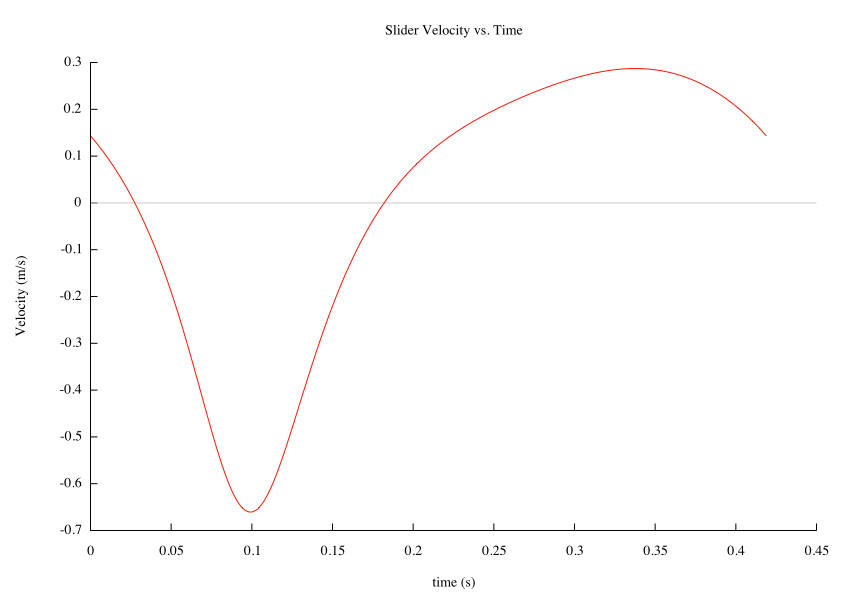
plots the velocity profile of the output slider, link 6. Figure 9 shows the velocity profile of the output slider after Program 1 has been executed. The last two lines
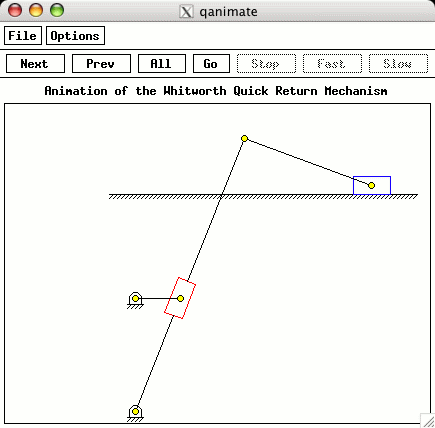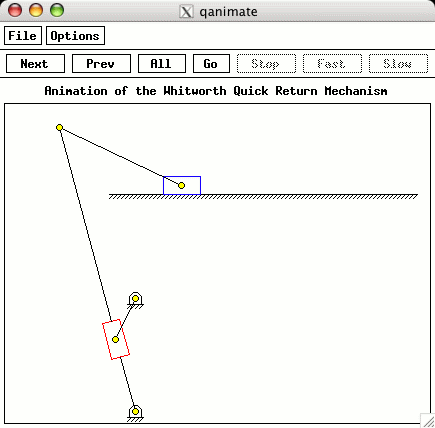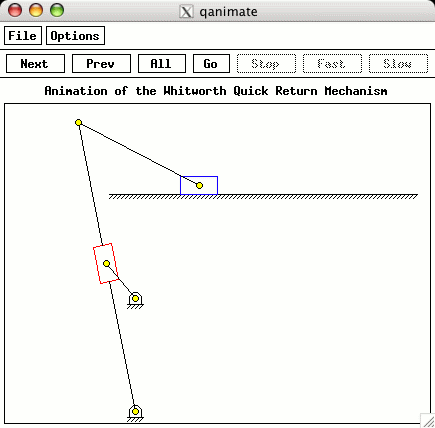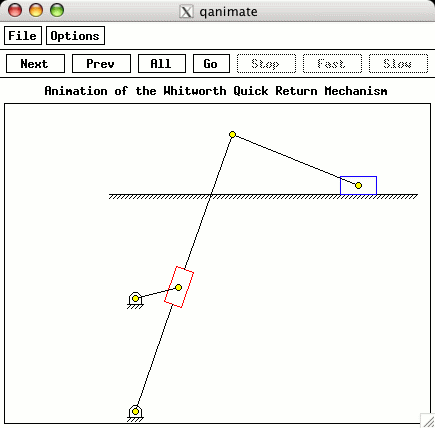
reset the number of points and create an animation shown below. Fewer points are used because the animation doesn't need as many as a plot to create decent output.
The results of running the above program are displayed below. The first is the velocity profile for the slider versus the time. The animation output is also shown.
To try out this analysis on the Web, you can use the Web-based interface to this code. The animation requires installation of Ch and its Mechanism Toolkit on your computer. The code that creates the class for the analysis of the Withworth quick return mechanisms can be obtained on the main page. It will allow you to run the analyses shown here on your own computer. It requires the same software, Ch and the Mechanism ToolKit.
The Ch software is free for academic users.
